Flexpool plot planner is wrong?

Chia Plotting
1

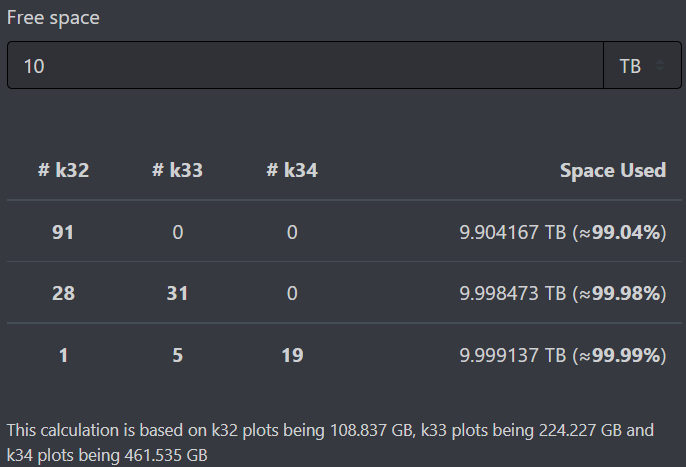
Although the k33 is equivalent to two k32 plots and has double chance to win, its size is slightly more than 2 x k32. k32 occupy approximately 108.837 GB and k33 224.227 GB. 224227 - 2 x 108837 = 6.553 MB. This size difference is not important on small scale but it’s important on large scale. For example you have 10 TB to plot. It has size of 91 k32 plots according to https://plot-plan.chia.foxypool.io/ If you want to have k33 plots besides those you should plot 31 k33 and 28 k32. If k33 plots have double chance to win than k32 we should multiply k33 plot size by 2. 31 x 2 = 62. Then we should add k32 plots. 62 + 28 = 90. In conclusion if we want to plot k33 besides k32 we have equivalent of 90 plots of k32 and if we want to plot only k32 we can plot 91. So 90 plots have less chance than 91 plots to win. Furthermore your chances of winning is worsen when you include k34 to the equation because 19 x 2 = 38 + 5 = 43 x 2 = 86 + 1 = 87. 91 plots vs equivalent of 87 plots. Please correct me if i’m wrong.

As a side note if this is true, does it mean the space occupied by plots is not important? The number of k32 plots are important?

2021-07-29 10_27_51-Chia Plot Plan

2

I believe your last statement is true, the raw size of the space isn’t critical, it is the number of plots. The idea of the plot planner seems to me too be based on a flawed belief that the network somehow sees raw space and rewards you for it.

If you really want to maximize storage used, one method would be to set some of your drives as an LVM volume group. An example of this would be you have 10x 8TB drives that can fit 72 plots each and each drive has 60gb left after being filled. 5 of the drives were created as LVM VGs, you then shrink the partition of the 5 drives that were not created as LVM VGs and create a second 60gb partition on those 5 drives. Add the new 60gb partitions to each VG, then expand each logical volume to fit the new size available. Now there’s enough room for an additional K32 plot, and if you lose one of those 2 drives, you only lose 1 additional plot rather than all plots. This setup is moderately complex, but not difficult.